电子档案
文章
第 3 卷 - 2015 年 12 月刊
抛丸器EDEM离散元仿真与分析
图1:EDEM中颗粒模型示意图
图2:EDEM中抛丸器主要工作零部件示意图
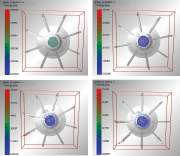
图3:弹丸进入抛丸器内0.1s-0.3s过程图
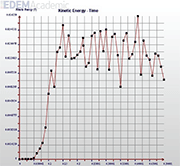
图4:弹丸运动过程平均能量 - 时间图
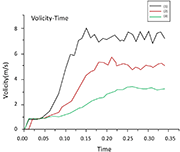
图5:弹丸平均速度拟合曲线
摘要:为了研究弹丸在抛丸器内运动对抛丸器的作用机理,以离散元为方法,建立了抛丸器离散元模型。以三维离散元软件EDEM为手段,对弹丸的运动过程进行宏观分析,通过模拟动态的展示了弹丸在抛丸器内运动的宏观规律。分析了弹丸运动过程的能量变化规律,以不同的分丸轮速度模拟测试弹丸的平均速度,发现分丸轮转速对弹丸平均速度的变化影响显著。关键词:抛丸器;离散元方法;模拟研究
目前抛丸器被广泛应用于各种加工工艺中,例如铸件的表面清理、零部件的表面强度提高、金属类板材的成型及金属构件的表面预处理。弹丸在抛丸器内的运动过程对于研究抛丸器来说十分重要,它属于离散物料的研究范畴,因此弹丸的运动过程研究本质上就是颗粒流的研究。
国内外有很多关于颗粒流的研究报道,国内,朴香兰[1]和王国强等用离散元方法对转送站物料转载过程进行了模拟研究,得出水平转弯输送物料时颗粒流的动力特性和物料颗粒对输送带的作用机理。张英爽[2]等利用离散元方法对转送站物料转载过程进行了模拟研究,分析得出了影响溜槽的各种因素。孙其诚[3]等基于严格的颗粒接触理论,利用离散元方法对准三维斜面颗粒流进行了数值模拟。国外,Alspaugh[4]等用离散元方法模拟了输送中物料转运问题。Savage[5]和Nedderman[6]等对平行竖直板组成的流道内颗粒流的速度分布进行了测定。Zhang[7]等利用离散元方法中改进的切向力-位移模型模拟了大豆在斜道上的流动,获得了大豆颗粒的速度分布图。但对于抛丸器内弹丸的运动过程研究,尚未见报道。因此以离散元理论为方法,以先进的离散元软件EDEM为手段,对弹丸在抛丸器内的运动过程进行了模拟分析,从而为今后抛丸器的优化设计提供参考依据。
1. 离散单元法
离散单元法(Distinct Element Method,简称 DEM)是一种不连续数值模拟方法。主要应用在采矿工程、岩土工程、材料力学、物料流动等领域。它的基本思想是把介质看做由一些独立并且离散的运动单元(颗粒)组成的,由这些离散物质所具有的离散性质建立数学模型,将需要分析的物体看做这些离散运动单元的集合,这样就可以使分析的物质与离散物质自身的特性一致。因此,离散单元法对分析离散体性质的物料运动时表现出极大的优越性。
抛丸器工作时,带动弹丸运动,在运动过程中,弹丸与弹丸之间,弹丸与抛丸器零部件之间都会发生碰撞,这些碰撞将决定弹丸在抛丸器内的运动规律。可以将弹丸的运动看为不连续的颗粒流动。离散单元法在离散体力学理论和牛顿第二定律的基础上,可以获得离散体在每个时步内的速度,位移和加速度,从而计算并模拟每个颗粒的运动状态,进而模拟离散体的运动,对于离散体颗粒较多的系统来说是理想的计算分析方法。
1.1 Hertz Mindlin无滑动接触模型(Hertz Mindlin (No Slip) Contact Model)
接触模型是离散单元法的核心,实质就是对颗粒固体在静态下的接触力进行模拟,分析接触力间弹塑性力学结果。对于不同的仿真对象,必须建立不同的接触类型。EDEM的接触模型库主要包括六种接触模型。Hertz Mindlin无滑动接触模型是EDEM默认的接触模型,也是需要用到的模型。
粒子与粒子之间,粒子与几何体面之间的产生的接触力都会被分解成两个力,一个是沿着接触法线方向的法向力,另一个是沿着接触平面的切向力。法向力可Fn由式求得[8]:
“公式无法显示” (1)
式中:R* — 粒子半径;
δn — 正常的交迭量;
Y* — 为等效杨氏模量。
法向阻尼力可以表示为:
“公式无法显示” (2)
式中:m* — 质量;
— 相对速度的常量。
若取e回弹系数,则β和Sn(硬度)可由下面两式计算得出:
“公式无法显示” (3)
“公式无法显示” (4)
切向力Ft跟切向交迭量δt和切向硬度St有关,可由下式表示:
“公式无法显示” (5)
“公式无法显示” (6)
式中:G* — 剪切模量。
切向阻尼系数为:
“公式无法显示” (7)
式中: — 切向相对速度。
切向力与摩擦力μsFn有关,这里μs是静摩擦系数。滚动摩擦系数在仿真中是很重要的,由接触表面上的力矩就可以表示,即:
τi = -μrFnRiωi (8)
式中:μr — 滚动摩擦系数;
Ri — 重心到接触点间的距离;
ωi — 接触点处物体的单位角速度。
1.2 运动方程 — 牛顿第二定律
由动力学理论可知,固体颗粒在空间坐标系中的运动主要由平动和转动两种方式构成,颗粒总的运动方式则可以视为两者的叠加。运动方程为[9]:
“公式无法显示” (9)
式中:mi — 颗粒i的质量;
— 颗粒i的角速度;
— 颗粒i的速度;
Ii — 颗粒i的转动惯量;
— 颗粒所受到的总作用力;
— 颗粒间碰撞而对颗粒i产生的扭矩的总和。
当颗粒j与颗粒i发生碰撞时,作用在颗粒i上的扭矩可由下式计算
“公式无法显示” (10)
式中: — 颗粒i的质心指向接触点的向量;
— 颗粒i,j的接触力。
如果在同一时刻有ki个颗粒与颗粒i接触,则颗粒i所受的总扭矩为。经过时间∆τ后颗粒i的速度和位置可分别由运动方程式积分后获得。
1.3 时步的确定
DEM的计算按时步进行,时步就是,整个粒子系统的运动时间过程,被看成若干时间段相叠加,这些时间段很小且相等,前提是假定单个时步内每个粒子的速度与加速度固定不变。由前面得到的合力、合力矩,再根据牛顿第二运动定律就可以得到块体质心的加速度和角加速度,从而可以得到在时步∆t内的速度、角速度、位移和转动惯量。
时步计算的优点是:(1)可以表示出系统中的不稳定因素。(2)需要很小的计算机内存就可以对巨大的粒子群体进行计算。运算过程中假设每个时步内各个粒子的速度和加速度是固定不变的,系统的运动状态可由时步运算方法数字化表示出来。
2. 数值模拟及结果分析
2.1 抛丸器弹丸流离散元模型的建立
首先,通过三维设计软件Solidworks建立所需的抛丸器几何体,包括分丸轮,定向套,叶轮和叶片,然后导入到离散元软件EDEM中,对弹丸的运动过程进行分析,分丸轮,定向套,叶片很大程度上决定了弹丸的运动轨迹,因此可以去掉抛丸器的壳体,只对主要影响部分建模,简化模型后分析。所取的颗粒单元如图1所示。所建立的离散元模型如图2所示,本文定义的物料为铸钢丸,它的泊松比为0.25,剪切模量为8e+10Pa,密度为7.8g/cm3,入料粒度为3mm,颗粒产生速率为40000/s个,由于现实中抛丸器内弹丸是不断加入的,因此这里设置弹丸连续生成,定义抛丸器各个部分的材料为钢材,泊松比为0.28,弹性模量为2.1e+5MPa,抗剪切模量为7.1e+4MPa,密度为7800Kg/m3。
2.2 数值模拟与分析
2.2.1 弹丸在抛丸器内运动过程的宏观模拟
本次仿真时间为5s,图3显示了弹丸在这5s内运动的宏观情况。图中红色线框部分为仿真计算域,用来模拟弹丸运动情况,颜色条代表弹丸的平均速度。
如图3所示为弹丸进入分丸轮内0.012s-0.3s过程图。设弹丸进入分丸轮内的初始速度为0.8m/s,这个速度取决于流丸管的高度,这里取初步估计的速度0.8m/s。弹丸从颗粒工厂中生成,落入旋转的分丸轮内,分丸轮的作用是加速弹丸,并把弹丸分开,0.01s时弹丸进入分丸轮内,刚刚进入分丸轮内的弹丸还没有被分开,随着分丸轮的高速旋转,弹丸被初步加速,0.07s时,一小部分弹丸从定向套窗口飞出,一小部分弹丸进入分丸轮和定向套的间隙中,间隙中的弹丸继续被加速,直至从定向套窗口飞出,此时颗粒的最大速度达到73.75m/s。随着分丸轮旋转,弹丸从定向套窗口飞出后,被叶片承接,被叶片继续加速后,脱离叶片,此时弹丸的最大速度可达到74.73m/s,与理论最大速度相符。
以上分析的弹丸在抛丸器内的运动规律与实际中弹丸的运动规律相符,且更能直观的表示出来,可视化程度高,在此基础上对其进行分析,可以方便的得到各因素对弹丸运动状态的影响。
2.2.2 弹丸运动过程中能量变化的模拟分析
弹丸首先进入分丸轮内,分丸轮带动其旋转,由弹丸的能量变化图可以看出在0.05s时获得初始能量,之后弹丸的能量继续增加,在0.05s-0.1s内弹丸运动的能量波动呈线性规律变化,从图3的分析可以得出,弹丸在这一阶段获得能量分两部分用途,一部分用于弹丸从定向套窗口抛出,一部分用于定向套与分丸轮间隙中的弹丸飞出定向套。
由理论分析知弹丸在分丸轮与定向套间隙中运动时,先进入的弹丸先被抛出,后进入的弹丸会形成一个数层弹丸的弹丸环,随着弹丸环的移动最终被抛出。由图4可以看出,弹丸由弹丸环内层向外层迁移过程,其实质是弹丸获得能量被加速的过程。0.1s之后弹丸的能量变化在一个小范围内波动,这是因为弹丸被抛丸轮叶片承接,能量继续增加,被承接的一部分弹丸被抛出后,弹丸的能量减小,后续弹丸又继续被叶片承接,能量又会增加,因此能量变化稳定在一定范围内波动。
2.2.3 不同的分丸轮转速对弹丸运动的影响
分丸轮分别以900rpm、 1500rpm和2600rpm的转速进行模拟,模拟时间3.5s,获得弹丸平均速度拟合后的曲线如图5所示,黑色(1)、红色(2)、绿色(3)曲线分别代表分丸轮转速为2600rpm、1500rpm和900rpm时弹丸平均速度曲线图,从图上可以看出,在模拟时间0-0.05s内弹丸的平均速度直线直线上升到某一个值,这是由于弹丸由进丸管进入,在重力加速度作用下使其进入分丸轮时有个初速度,虽然这个是抛丸器的简化模型,没有进丸管,但可以通过计算后,由软件设定这个值进行模拟,模拟结果与实际过程相符合。
0.05s-0.08s之间,弹丸主要在分丸轮的带动下运动,弹丸的速度变化成线性变化规律,且分丸轮转速越大,速度变化速率越大,因此分丸轮转速对弹丸速度的影响是显著的。0.08s之后,弹丸由定向套窗口飞出,被抛丸叶片承接,进一步加速,此时弹丸平均速度变化成线性增长,而且变化时间较长,可以看出这段时间对弹丸的速度变化起决定性的作用。还可以看出,分丸轮转速越大,弹丸的平均速度的最大值越大,达到最大值后弹丸的平均速度基本不变,在这个值附近上下波动,而且分丸轮转速越大,波动的幅度越大。这在一定程度上说明了,分丸轮转速与弹丸平均速度之间的内在关联性。
3. 结论
1)弹丸进入分丸轮后,一部分能量用于飞出定向套,另一部分能量用于分丸轮与定向套间隙中的弹丸飞出定向套,且这部分能量的变化通过弹丸层的运动变化传递,最终使弹丸飞出定向套。
2)以不同的分丸轮转速,模拟弹丸在抛丸器内的运动规律,发现分丸轮转速越大,弹丸平均速度和速度的最大值越大,而且速度变化率越大。说明了分丸轮转速对弹丸平均速度的显著影响。
3)借助DEM的优势,宏观模拟和显示了弹丸流在抛丸器内动态的运动过程。而且还可以获得不同时刻,不同位置弹丸的运动状态。从理论上分析弹丸流的运动状态对抛丸器的影响,从而为抛丸器的优化设计提供参考依据。
参考文献
[1]朴香兰,王国强,张占强,等.水平转弯颗粒流的离散元模拟[J].吉林大学学报,2010,1(40): 98-102.
[2]朴香兰,王国强,张英爽.转送站的离散元模拟研究[J].矿山机械,2009,23(37):57-60.
[3]孙其诚,王光谦.斜面颗粒流的离散元模拟[C]//中国科学技术学会2008防灾减灾论坛论文集,北京:中国科学技术协会,2008:12-17.
[4]Alspause M,Dewicki G,Quesenberry E.Computer simulation solves conveyor problems[J].Coal Age,2002(1):28-31.
[5]Savage S B.Gravity flow of cohensionless granular material in chutes and channels[J]. JFM, 1979, 92:53-96.
[6]Nedderman R M,Laohakul C.The thickness of the shear zone of the flowing granular materials [J].Powder Tech,1980,25:91-100.
[7]Zhang X,Vu Quoc L.Simulation of chute flow of soybeans using an improved tangential force displacenent model[J].Mechanics of Materials,2000,32:115-129.
[8]王国强,郝万军,王继新.离散单元法及其在EDEM上的实践[M].西安:西北工业大学出社, 2010.5.
[9]李媛华,基于离散元技术的球磨机参数优化研究[D].长春:吉林大学,2009.
王守仁教授
济南大学机械工程学院
电话:18905431989
邮箱:sherman0158@163.com
徐金成、王瑞国、张肖
山东开泰抛丸机械有限公司
中国山东邹平县青阳镇驻地(邮编:256217)










